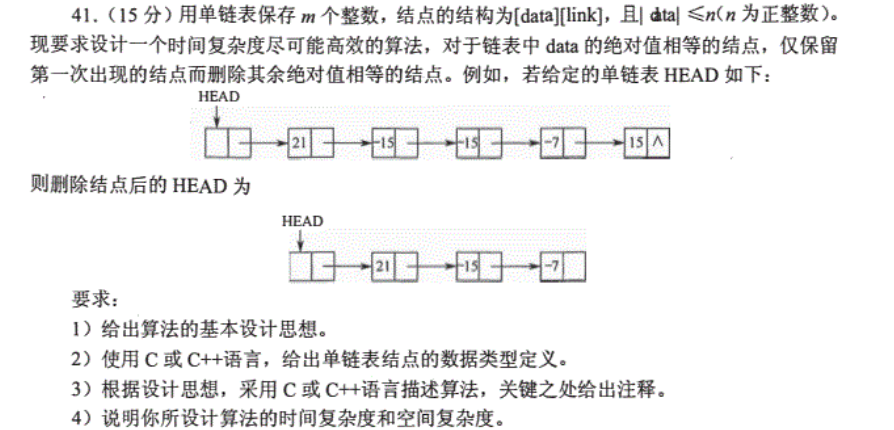
一、题目描述

    已知一个整数序列A(a0····an)，其中0<=ain/2，则称x为A序列的主元素。
    例如：0 5 5  3 5 7 5 5的主元素为5
    0 5 5 3 5 1 5 7没有主元素
    假设A中的元素都在一个一维数组中，请设计一个尽可能高效的算法，找出A的主元素，若主元素则输出它，不存在则输出-1。

二、算法步骤

首先理解题意，注意到每个元素均大于等于0，且元素的值不会大于序列长度，什么意思？假设该序列的长度为10，则其中的每个元素的值一定大于等于0且小于10，这其实是一个暗示。接着我们需要找到一个序列中数量大于n/2的相等元素，也就是说该序列中有一半多的元素相等，此时我们称该序列有主元素。
现在如何做到？我们另开一个数组b，用于记录a中元素出现的次数，只要a中的某个元素出现，那么b中该元素出现的次数++：b[a[i]]++。
最后从头到尾扫描一遍b数组，找出次数大于n/2的元素即可:
if(b[i]>=n/2+1)；循环条件是i<n ，此时之前的题目暗示也就起作用了。代码如下：

#include 
using namespace std;
const int N = 10;//假设最大的数组长度为10
int n;
int a[N], b[N];
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    cin >> n;
    for (int i = 0; i < n; i++) { cin >> a[i]; }
    for (int i = 0; i < n; i++)
    {
        b[a[i]]++; //记录该数出现的次数，a[i]表示该数
    }
    int ans = -1;
    for (int i = 0; i < n; i++)
    {
        if (b[i] >= n / 2 + 1) { ans = i; }//获取主元素
    }
    cout << ans;
    return 0;
}

结果展示：

8
0 5 5 3 5 7 5 5
5

显然该算法的时空复杂度为O(N);

三、总结

本题关键是记录每个数出现的次数，好在题目足够友好，所有整数均>=0且数值小于序列长度，否则可能需要考虑离散化的做法。总的来说比较简单。