一、题目描述

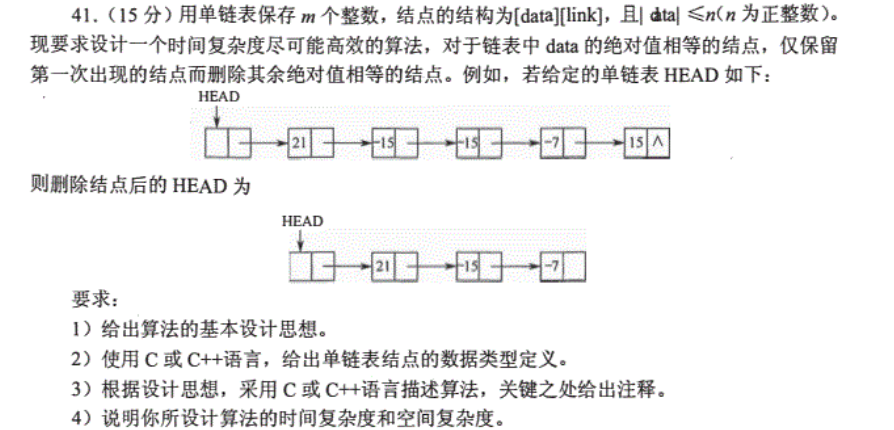
给定一个含n(n>=1)个整数的数组，请选择一个时间上和空间上尽可能高效的算法，找出该数组中未出现的最小正整数。
例如-5 3 2 3 中未出现的最小正整数是1，数组1 2 3中未出现的最小正整数是4。要求给出算法步骤和时空复杂度。

二、算法步骤

本题也可以采用开辅助数组的做法，首先记录数组a中每个数出现的次数，放入数组b中，然后从1开始遍历数组b，循环条件为i<=n+1,n为数组长度，因为n个数中最小正整数的最坏的情况就是1~n都有，n+1没有，因此需要到多一位，此外假设数列为1 2 19999，虽然19999出现了，但是3没出现，因此我们仍然可以在i<=n+1中找到想要的答案3，不需要i<19999。
相关代码如下：

#include <iostream>
using namespace std;
const int N = 10;//假设最大的数组长度为10
int n;
int a[N], b[N];
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    cin >> n;
    for (int i = 0; i < n; i++) { cin >> a[i]; }
    for (int i = 0; i < n; i++)
    {
        if (a[i] > 0) { b[a[i]]++; }
    }
    for (int i = 1; i <= n+1; i++)
    {
        if (b[i] == 0) { cout << i; break; }
    }
    return 0;
}

结果：

4
-5 3 2 3
1

3
1 2 3
4

显然，该算法的时空复杂度均为O(N);

三、总结

本题较为简单，主要是能想清楚最后b数组的循环条件是:
for(int i =1;i<=n+1;i++)即可，