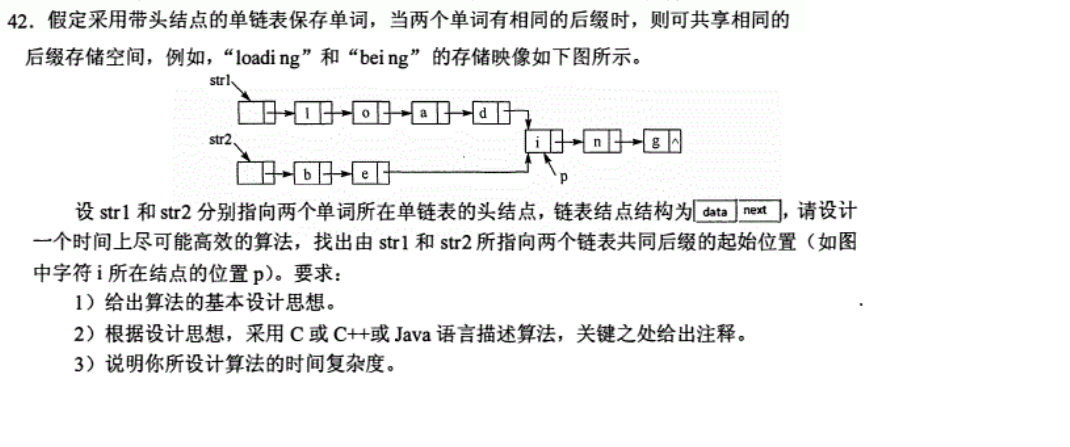
一、题目描述

    一个长度为L(L>=1)的升序序列S，在其第[L/2]个位置的数称为S的中位数。例如S1：11 13 15 17 19，则其中位数为15。两个数的中位数是含他们所有元素的升序序列的中位数，例如S2为 2 4 6 8 20，则S1S2的中位数是11。
    现有两个等长的升序序列A、B，请设计一个时间和空间尽可能高效的算法，找到两个序列AB的中位数，并说出设计算法的时空复杂度。

二、算法步骤

题目例子中S1S2的中位数的获取首先需要S1S2进行排序：
1 4 6 8 11 13 15 17 19 20，此时共有10个数，中间的数是10/2=5，对应11，在数组中则是第5-1=4个下标。
首先进行排序，采用双指针算法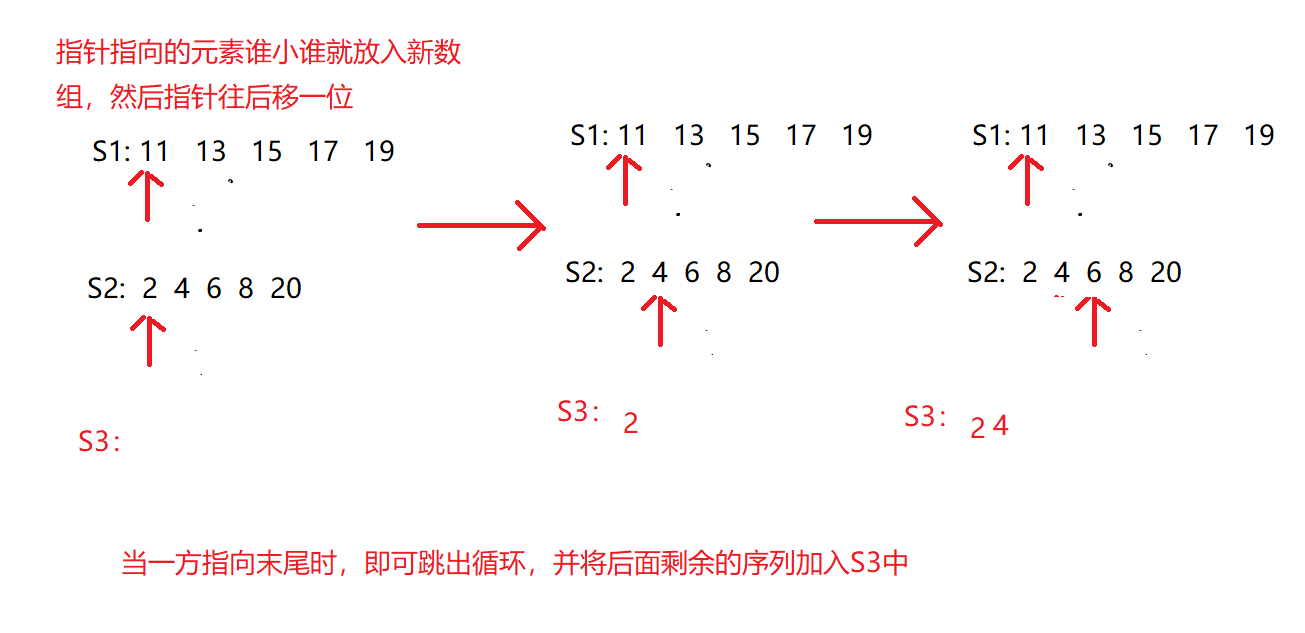：。代码如下：

#include <iostream>
using namespace std;
const int N = 10;
int n, p;
int a[N], b[N], s[N];
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    cin >> n;
    for (int i = 0; i < n; i++) { cin >> a[i]; }
    for (int i = 0; i < n; i++) { cin >> b[i]; }

    int i = 0, j = 0,k=0;
    while (i < n && j < n)
    {
        if (i < n) //防越界
        {
            if (a[i] == b[j]) { s[k++] = a[i]; i++; j++; }//相等额外处理，俩指针同时++
            if (a[i] < b[j]) { s[k++] = a[i]; i++; }//谁小就放在S中
        }
        if (j < n)
        {   
            if (a[i] == b[j]) { s[k++] = b[j]; i++; j++; }
            if (b[j] < a[i]) { s[k++] = b[j]; j++; }
        }
    }
    while (i < n || j < n)
    {
        if (i < n) { s[k++] = a[i++]; }
        if (j < n) { s[k++] = b[j++]; }
    }
    for (int i = 0; i < n + n; i++) { cout << s[i] << " "; }//可打印一下合并后的数组
    cout << endl;
    cout << s[(n+n) / 2 - 1];//输出题目要求答案
    return 0;
}

//结果
5
11 13 15 17 19
2 4 6 8 20
2 4 6 8 11 13 15 17 19 20
11

显然，该算法时间复杂度为O(N)，空间复杂度为O(N)；

三、总结

本题难点在于对两个有序数组进行合并，可以选择无脑合并然后排序，时间复杂度取决于排序的方式，也可以利用两个有序数组的特性，使用双指针排序，时间复杂度更低。